Equations of Motion - Linear, Circular and Projectile

To be able to describe the motion of a body in mathematical terms, we must first understand the type of motion it is undergoing. The equation(s) of motion to be used will vary depending on the situation under consideration.

1. Linear motion

There are three general cases of linear motion characterised by the type of acceleration it is undergoing.

No acceleration or deceleration – Constant speed

If the object’s speed is fixed at all times, then it does not experience any acceleration or deceleration at all. Its speed will remain constant as time changes. Remember that there may or may not be forces acting on it but there is no net force causing it to accelerate. The equation of motion used in this case is simple, in the form of:

\(v=s/t\)

where,

\(v\): speed or velocity (in m/s or ft/s)

\(s\): distance travelled or displacement (in m or ft)

\(t\): time taken to travel that distance (in s)

Example 1

A person takes 10 minutes to walk from point A to point B. Calculate the distance separating the two points, assuming that he walks at a constant speed of 1.5 m/s the whole time.

Answer: First, the time taken needs to be converted to seconds to remain consistent with units. By plugging in the values into the equation, we then get a distance of 900 m.

Constant acceleration or deceleration – Varying Speed

In this case, the body accelerates at a constant rate throughout its motion. The speed it travels will therefore change as time advances.

Typical graphs for this type of motion are as shown below.

The following formula of motion are then used:

\(v=u+at\)

\(s=ut+\frac{1}{2}at^2\)

\(v^2=u^2+2as\)

where,

\(v\): final velocity (m/s)

\(u\): initial velocity (m/s)

\(a\): rate of acceleration. If body is in deceleration, then use a minus sign (\(m/s^2\))

\(t\): time taken (s)

\(s\): distance travelled (m)

Example 2

An object is held at rest 12 m above the ground. The object is released at time \(t=0 s\) and falls freely under gravity. Given that the acceleration due to gravity is 9.81 \(m/s^2\), find its speed midway between its starting point and the ground.

Answer: Using the third formula of motion (\(v^2=u^2+2as\)) and the quantities \(a=9.81 m/s^2 \), \(s=6m\), \(u=0 m/s\); we then get an answer of 10.85 m/s.

Varying Acceleration

Each object undergoing this type of motion will have a specific equation describing its displacement, velocity and acceleration at specific points in time. By knowing one of these equations, it is possible to determine the others by integrating or differentiating with respect to time. For this type of motion, it is important to keep in mind the following:

Speed (\(v\)) is the rate of change of distance (\(s\)) with time (\(t\)) or in calculus terms: \(\frac{ds}{dt}\)
Acceleration (\(a\)) is the rate of change of speed (\(v\)) with time (\(t\)) or in calculus terms: \(\frac{{d^2}s}{d{t^2}}\)

Example 3

A particle moves in space with its speed given by the equation \(v= 4t^3 + 6\). Find its speed, distance travelled and acceleration at time t = 5 s.

Answer: The speed can be found easily by plugging t = 5 s in the above equation, giving \(v=506 m/s\). The acceleration can also be found by differentiating \(v\) and using t = 5 s. To find the distance travelled, we need to integrate \(v\) using limits of t = 0s and t = 5 s.

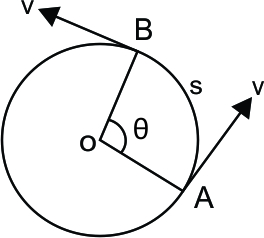
2. Circular Motion

Consider a body that is moving in circular motion about point O as shown below.

If the body takes a time \(t\) to make an angle \(\theta\) about point O, then we can find its angular speed using:

\(\omega = \theta/t\)

The period \(T\) for the object to complete a full revolution is given by:

\(T = \frac{2\pi}{\omega}\)

The distance travelled \(s\) is calculated using:

\(s = r\theta\)

The linear speed can also be found by dividing the last equation by time taken \(t\):

\(\frac{s}{t} = r\frac{\theta}{t}\)

\(v = r\omega\)

For the body to remain in circular motion, there needs to be a force pulling it towards the centre. Otherwise, the object will move out of orbit in a straight line according to Newton’s First law of motion. This force is also known as the centripetal force and it induces an acceleration on the body. The direction of the acceleration is towards the centre which is the same as that of the centripetal force. The centripetal acceleration can be calculated as:

\(a = \frac{v^2}{r}\)

\(a = r\omega^2\)

3. Projectile Motion

The motion of a projectile thrown at an angle \(x\) degrees relative to the ground is shown below.

The velocity vector \(u\) can be decomposed to its 2 components \(u_x\) and \(u_y\).

\(u_x = u\cos{x}\)

\(u_y = u\sin{x}\)

As soon as a projectile is released, its trajectory will depend on two things: its initial velocity and the acceleration due to gravity.

Equations of Motion – Linear, Circular and Projectile